Chapter 2- Polynomials Exercise 2.2 – NCERT Solutions for class 10 Maths
Chapter 2- Polynomials Exercise 2.2 – NCERT Solutions for class 10 Maths
These solutions are produced by math professionals who have had them evaluated on a regular basis. Students can use these NCERT chapter-by-chapter solutions to study and prepare for their CBSE board exams.

Question 1. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and their coefficients:
(i) x2 – 2x – 8
x2 − 4x + 2x − 8 = 0
x(x−4) + 2(x−4) = 0
(x−4)(x+2) = 0
(x−4) = 0, (x+2) = 0
x = 4, x = −2 are the zeroes of the polynomial
Relationship between the zeroes and the coefficients
Sum of zeroes = −coefficient of x / coefficient of x2
α + β = −b/a
−2+4 = − (−2)/1
2 = 2
Product of zeroes = constant term / coefficient of x2
α.β = c/a
−2×4 = −8/1
−8 = −8
Hence, Verified.
(ii) 4s2 – 4s + 1
4s2−2s−2s+1= 0
2s(2s−1)−(2s−1) = 0
(2s−1)(2s−1) = 0
2s−1= 0, 2s−1 = 0
s =1/2, s = 1/2 are the zeroes of the polynomial.
Relationship between the zeroes and the coefficients
Sum of zeroes =−coefficient of x / coefficient of x2
α + β = −b/a
1/2 + 1/2 = −(−4)/4
1 = 1
Product of zeroes = constant term / coefficient of x2
α.β = c/a
1/2×1/2 = 1/4
1/4 = 1/4
Hence, Verified.
(iii) 6x2 – 3 – 7x
6x2−7x−3 = 0
6x2−9x+2x−3 = 0
3x(2x−3)+(2x−3) = 0
(2x−3) = 0, (3x+1) = 0
x = 3/2, x = −1/3 are the zeroes of the polynomial
Relationship between the zeroes and the coefficients
Sum of zeroes =− coefficient of x / coefficient of x2
α + β = −b/a
α + β = −(−7)/6
3/2 + −1/3 = (7)/6
7/6 = 7/6
Product of zeroes = constant term / coefficient of x2
α.β = c/a
3/2 × −1/3 = (−3)/6
(−3)/6 = (−3)/6
(−1)/2 = (−1)/2
Hence, Verified.
(iv) 4u2 + 8u
4u(u+2) = 0
4u = 0 or u+2 = 0
u = 0 or u = −2 are the zeroes of the polynomial
Relationship between the zeroes and the coefficients
Sum of zeroes =− coefficient of x / coefficient of x2
α + β = −b/a
α + β = −(8)/4
0+(−2) =−2
−2 =−2
Product of zeroes = constant term / coefficient of x2
α.β = c/a
0 ×−2 = 0/4
0 = 0
Hence, Verified.
(v) t2 – 15
t2−15 = 0
t = √15
t = −√15, t = +√15 are the zeroes of the polynomial
Relationship between the zeroes and the coefficients
Sum of zeroes =− coefficient of x / coefficient of x2
α + β =−b/a
α + β = 0/1
−√15+√15 = 0
0 = 0
Product of zeroes = constant term / coefficient of x2
α.β = c/a
−√15 ×√15 =−15/1
−15=−15
Hence, Verified.
(vi) 3x2 – x – 4
3x2−x−4 = 0
3x2−4x+3x−4 = 0
x(3x−4)+(3x−4) = 0
(x+1)(3x−4) = 0
(x+1) = 0 or (3x−4) = 0
x =−1 or x = 4/3 are the zeroes of the polynomial
Relationship between the zeroes and the coefficients
Sum of zeroes =− coefficient of x / coefficient of x2
α + β =−1/3
−1+4/3=−1/3
1/3=1/3
Product of zeroes = constant term / coefficient of x2
α.β = c/a
−1×4/3=−4/3
−4/3=−4/3
Hence, Verified.
Question 2. Find a quadratic polynomial each with the given numbers as the sum and product of zeroes respectively:
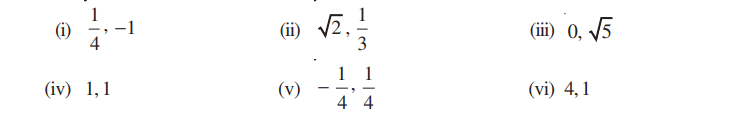
(i) 1/4 , -1
From the formulas of sum and product of zeroes, we know,
Sum of zeroes = α+β
Product of zeroes = α .β
Sum of zeroes = α+β = 1/4
Product of zeroes = α β = -1
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as :-
x2−(sum of roots)x + product of roots = 0
x2–(α+β)x +αβ = 0
x2–(1/4)x +(-1) = 0
4x2–x-4 = 0
Thus, 4x2–x–4 is the quadratic polynomial.
(ii)√2, 1/3
Sum of zeroes = α + β =√2
Product of zeroes = α β = 1/3
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2−(sum of roots)x + product of roots = 0
x2–(α+β)x +αβ = 0
x2 –(√2)x + (1/3) = 0
3x2-3√2x+1 = 0
Thus, 3x2-3√2x+1 is the quadratic polynomial.
(iii) 0, √5
Given, Sum of zeroes = α+β = 0
Product of zeroes = α β = √5
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2−(sum of roots)x + product of roots = 0
x2–(α+β)x +αβ = 0
x2–(0)x +√5= 0
Thus, x2+√5 is the quadratic polynomial.
(iv) 1, 1
Given, Sum of zeroes = α+β = 1
Product of zeroes = α β = 1
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as :-
x2−(sum of roots)x + product of roots = 0
x2–(α+β)x +αβ = 0
x2–x+1 = 0
Thus , x2–x+1 is the quadratic polynomial.
(v) -1/4, 1/4
Given, Sum of zeroes = α+β = -1/4
Product of zeroes = α β = 1/4
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as :-
x2−(sum of roots)x + product of roots = 0
x2–(α+β)x +αβ = 0
x2–(-1/4)x +(1/4) = 0
4x2+x+1 = 0
Thus,4x2+x+1 is the quadratic polynomial.
(vi) 4, 1
Given, Sum of zeroes = α+β =
Product of zeroes = αβ = 1
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2−(sum of roots)x + product of roots = 0
x2–(α+β)x+αβ = 0
x2–4x+1 = 0
Thus, x2–4x+1 is the quadratic polynomial.
